Note
Go to the end to download the full example code
Tutorial 4: Train SimSiam on Satellite Images
In this tutorial we will train a SimSiam model in old-school PyTorch style on a set of satellite images of Italy. We will showcase how the generated embeddings can be used for exploration and better understanding of the raw data.
You can read up on the model in the paper Exploring Simple Siamese Representation Learning.
We will be using a dataset of satellite images from ESAs Sentinel-2 satellite over Italy. If you’re interested, you can get your own data from the Copernicus Open Acces Hub. The original images have been cropped into smaller tiles due to their immense size and the dataset has been balanced based on a simple clustering of the mean RGB color values to prevent a surplus of images of the sea.
In this tutorial you will learn:
How to work with the SimSiam model
How to do self-supervised learning using PyTorch
How to check whether your embeddings have collapsed
Imports
Import the Python frameworks we need for this tutorial.
import math
import numpy as np
import torch
import torch.nn as nn
import torchvision
from lightly.data import LightlyDataset
from lightly.loss import NegativeCosineSimilarity
from lightly.models.modules.heads import SimSiamPredictionHead, SimSiamProjectionHead
from lightly.transforms import SimCLRTransform, utils
Configuration
We set some configuration parameters for our experiment.
The default configuration with a batch size and input resolution of 256 requires 16GB of GPU memory.
num_workers = 8
batch_size = 128
seed = 1
epochs = 50
input_size = 256
# dimension of the embeddings
num_ftrs = 512
# dimension of the output of the prediction and projection heads
out_dim = proj_hidden_dim = 512
# the prediction head uses a bottleneck architecture
pred_hidden_dim = 128
Let’s set the seed for our experiments and the path to our data
# seed torch and numpy
torch.manual_seed(0)
np.random.seed(0)
# set the path to the dataset
path_to_data = "/datasets/sentinel-2-italy-v1/"
Setup data augmentations and loaders
Since we’re working on satellite images, it makes sense to use horizontal and vertical flips as well as random rotation transformations. We apply weak color jitter to learn an invariance of the model with respect to slight changes in the color of the water.
# define the augmentations for self-supervised learning
transform = SimCLRTransform(
input_size=input_size,
# require invariance to flips and rotations
hf_prob=0.5,
vf_prob=0.5,
rr_prob=0.5,
# satellite images are all taken from the same height
# so we use only slight random cropping
min_scale=0.5,
# use a weak color jitter for invariance w.r.t small color changes
cj_prob=0.2,
cj_bright=0.1,
cj_contrast=0.1,
cj_hue=0.1,
cj_sat=0.1,
)
# create a lightly dataset for training with augmentations
dataset_train_simsiam = LightlyDataset(input_dir=path_to_data, transform=transform)
# create a dataloader for training
dataloader_train_simsiam = torch.utils.data.DataLoader(
dataset_train_simsiam,
batch_size=batch_size,
shuffle=True,
drop_last=True,
num_workers=num_workers,
)
# create a torchvision transformation for embedding the dataset after training
# here, we resize the images to match the input size during training and apply
# a normalization of the color channel based on statistics from imagenet
test_transforms = torchvision.transforms.Compose(
[
torchvision.transforms.Resize((input_size, input_size)),
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
mean=utils.IMAGENET_NORMALIZE["mean"],
std=utils.IMAGENET_NORMALIZE["std"],
),
]
)
# create a lightly dataset for embedding
dataset_test = LightlyDataset(input_dir=path_to_data, transform=test_transforms)
# create a dataloader for embedding
dataloader_test = torch.utils.data.DataLoader(
dataset_test,
batch_size=batch_size,
shuffle=False,
drop_last=False,
num_workers=num_workers,
)
Create the SimSiam model
Create a ResNet backbone and remove the classification head
class SimSiam(nn.Module):
def __init__(self, backbone, num_ftrs, proj_hidden_dim, pred_hidden_dim, out_dim):
super().__init__()
self.backbone = backbone
self.projection_head = SimSiamProjectionHead(num_ftrs, proj_hidden_dim, out_dim)
self.prediction_head = SimSiamPredictionHead(out_dim, pred_hidden_dim, out_dim)
def forward(self, x):
# get representations
f = self.backbone(x).flatten(start_dim=1)
# get projections
z = self.projection_head(f)
# get predictions
p = self.prediction_head(z)
# stop gradient
z = z.detach()
return z, p
# we use a pretrained resnet for this tutorial to speed
# up training time but you can also train one from scratch
resnet = torchvision.models.resnet18()
backbone = nn.Sequential(*list(resnet.children())[:-1])
model = SimSiam(backbone, num_ftrs, proj_hidden_dim, pred_hidden_dim, out_dim)
SimSiam uses a symmetric negative cosine similarity loss and does therefore not require any negative samples. We build a criterion and an optimizer.
# SimSiam uses a symmetric negative cosine similarity loss
criterion = NegativeCosineSimilarity()
# scale the learning rate
lr = 0.05 * batch_size / 256
# use SGD with momentum and weight decay
optimizer = torch.optim.SGD(model.parameters(), lr=lr, momentum=0.9, weight_decay=5e-4)
Train SimSiam
To train the SimSiam model, you can use a classic PyTorch training loop: For every epoch, iterate over all batches in the training data, extract the two transforms of every image, pass them through the model, and calculate the loss. Then, simply update the weights with the optimizer. Don’t forget to reset the gradients!
Since SimSiam doesn’t require negative samples, it is a good idea to check whether the outputs of the model have collapsed into a single direction. For this we can simply check the standard deviation of the L2 normalized output vectors. If it is close to one divided by the square root of the output dimension, everything is fine (you can read up on this idea here).
device = "cuda" if torch.cuda.is_available() else "cpu"
model.to(device)
avg_loss = 0.0
avg_output_std = 0.0
for e in range(epochs):
for (x0, x1), _, _ in dataloader_train_simsiam:
# move images to the gpu
x0 = x0.to(device)
x1 = x1.to(device)
# run the model on both transforms of the images
# we get projections (z0 and z1) and
# predictions (p0 and p1) as output
z0, p0 = model(x0)
z1, p1 = model(x1)
# apply the symmetric negative cosine similarity
# and run backpropagation
loss = 0.5 * (criterion(z0, p1) + criterion(z1, p0))
loss.backward()
optimizer.step()
optimizer.zero_grad()
# calculate the per-dimension standard deviation of the outputs
# we can use this later to check whether the embeddings are collapsing
output = p0.detach()
output = torch.nn.functional.normalize(output, dim=1)
output_std = torch.std(output, 0)
output_std = output_std.mean()
# use moving averages to track the loss and standard deviation
w = 0.9
avg_loss = w * avg_loss + (1 - w) * loss.item()
avg_output_std = w * avg_output_std + (1 - w) * output_std.item()
# the level of collapse is large if the standard deviation of the l2
# normalized output is much smaller than 1 / sqrt(dim)
collapse_level = max(0.0, 1 - math.sqrt(out_dim) * avg_output_std)
# print intermediate results
print(
f"[Epoch {e:3d}] "
f"Loss = {avg_loss:.2f} | "
f"Collapse Level: {collapse_level:.2f} / 1.00"
)
[Epoch 0] Loss = -0.86 | Collapse Level: 0.17 / 1.00
[Epoch 1] Loss = -0.89 | Collapse Level: 0.14 / 1.00
[Epoch 2] Loss = -0.89 | Collapse Level: 0.12 / 1.00
[Epoch 3] Loss = -0.91 | Collapse Level: 0.10 / 1.00
[Epoch 4] Loss = -0.92 | Collapse Level: 0.10 / 1.00
[Epoch 5] Loss = -0.94 | Collapse Level: 0.08 / 1.00
[Epoch 6] Loss = -0.94 | Collapse Level: 0.08 / 1.00
[Epoch 7] Loss = -0.95 | Collapse Level: 0.08 / 1.00
[Epoch 8] Loss = -0.95 | Collapse Level: 0.08 / 1.00
[Epoch 9] Loss = -0.95 | Collapse Level: 0.08 / 1.00
[Epoch 10] Loss = -0.95 | Collapse Level: 0.07 / 1.00
[Epoch 11] Loss = -0.95 | Collapse Level: 0.08 / 1.00
[Epoch 12] Loss = -0.95 | Collapse Level: 0.10 / 1.00
[Epoch 13] Loss = -0.95 | Collapse Level: 0.09 / 1.00
[Epoch 14] Loss = -0.95 | Collapse Level: 0.11 / 1.00
[Epoch 15] Loss = -0.95 | Collapse Level: 0.10 / 1.00
[Epoch 16] Loss = -0.94 | Collapse Level: 0.10 / 1.00
[Epoch 17] Loss = -0.94 | Collapse Level: 0.12 / 1.00
[Epoch 18] Loss = -0.94 | Collapse Level: 0.13 / 1.00
[Epoch 19] Loss = -0.94 | Collapse Level: 0.12 / 1.00
[Epoch 20] Loss = -0.93 | Collapse Level: 0.12 / 1.00
[Epoch 21] Loss = -0.94 | Collapse Level: 0.14 / 1.00
[Epoch 22] Loss = -0.94 | Collapse Level: 0.14 / 1.00
[Epoch 23] Loss = -0.94 | Collapse Level: 0.14 / 1.00
[Epoch 24] Loss = -0.95 | Collapse Level: 0.14 / 1.00
[Epoch 25] Loss = -0.95 | Collapse Level: 0.14 / 1.00
[Epoch 26] Loss = -0.95 | Collapse Level: 0.13 / 1.00
[Epoch 27] Loss = -0.95 | Collapse Level: 0.12 / 1.00
[Epoch 28] Loss = -0.95 | Collapse Level: 0.12 / 1.00
[Epoch 29] Loss = -0.95 | Collapse Level: 0.14 / 1.00
[Epoch 30] Loss = -0.95 | Collapse Level: 0.13 / 1.00
[Epoch 31] Loss = -0.95 | Collapse Level: 0.13 / 1.00
[Epoch 32] Loss = -0.96 | Collapse Level: 0.13 / 1.00
[Epoch 33] Loss = -0.95 | Collapse Level: 0.11 / 1.00
[Epoch 34] Loss = -0.96 | Collapse Level: 0.11 / 1.00
[Epoch 35] Loss = -0.95 | Collapse Level: 0.11 / 1.00
[Epoch 36] Loss = -0.95 | Collapse Level: 0.10 / 1.00
[Epoch 37] Loss = -0.95 | Collapse Level: 0.10 / 1.00
[Epoch 38] Loss = -0.95 | Collapse Level: 0.09 / 1.00
[Epoch 39] Loss = -0.96 | Collapse Level: 0.09 / 1.00
[Epoch 40] Loss = -0.96 | Collapse Level: 0.09 / 1.00
[Epoch 41] Loss = -0.96 | Collapse Level: 0.07 / 1.00
[Epoch 42] Loss = -0.96 | Collapse Level: 0.07 / 1.00
[Epoch 43] Loss = -0.95 | Collapse Level: 0.06 / 1.00
[Epoch 44] Loss = -0.95 | Collapse Level: 0.07 / 1.00
[Epoch 45] Loss = -0.95 | Collapse Level: 0.05 / 1.00
[Epoch 46] Loss = -0.95 | Collapse Level: 0.04 / 1.00
[Epoch 47] Loss = -0.96 | Collapse Level: 0.05 / 1.00
[Epoch 48] Loss = -0.96 | Collapse Level: 0.04 / 1.00
[Epoch 49] Loss = -0.96 | Collapse Level: 0.03 / 1.00
To embed the images in the dataset we simply iterate over the test dataloader and feed the images to the model backbone. Make sure to disable gradients for this part.
embeddings = []
filenames = []
# disable gradients for faster calculations
model.eval()
with torch.no_grad():
for i, (x, _, fnames) in enumerate(dataloader_test):
# move the images to the gpu
x = x.to(device)
# embed the images with the pre-trained backbone
y = model.backbone(x).flatten(start_dim=1)
# store the embeddings and filenames in lists
embeddings.append(y)
filenames = filenames + list(fnames)
# concatenate the embeddings and convert to numpy
embeddings = torch.cat(embeddings, dim=0)
embeddings = embeddings.cpu().numpy()
Scatter Plot and Nearest Neighbors
Now that we have the embeddings, we can visualize the data with a scatter plot. Further down, we also check out the nearest neighbors of a few example images.
As a first step, we make a few additional imports.
# for plotting
import os
import matplotlib.offsetbox as osb
import matplotlib.pyplot as plt
# for resizing images to thumbnails
import torchvision.transforms.functional as functional
from matplotlib import rcParams as rcp
from PIL import Image
# for clustering and 2d representations
from sklearn import random_projection
Then, we transform the embeddings using UMAP and rescale them to fit in the [0, 1] square.
# for the scatter plot we want to transform the images to a two-dimensional
# vector space using a random Gaussian projection
projection = random_projection.GaussianRandomProjection(n_components=2)
embeddings_2d = projection.fit_transform(embeddings)
# normalize the embeddings to fit in the [0, 1] square
M = np.max(embeddings_2d, axis=0)
m = np.min(embeddings_2d, axis=0)
embeddings_2d = (embeddings_2d - m) / (M - m)
Let’s start with a nice scatter plot of our dataset! The helper function below will create one.
def get_scatter_plot_with_thumbnails():
"""Creates a scatter plot with image overlays."""
# initialize empty figure and add subplot
fig = plt.figure()
fig.suptitle("Scatter Plot of the Sentinel-2 Dataset")
ax = fig.add_subplot(1, 1, 1)
# shuffle images and find out which images to show
shown_images_idx = []
shown_images = np.array([[1.0, 1.0]])
iterator = [i for i in range(embeddings_2d.shape[0])]
np.random.shuffle(iterator)
for i in iterator:
# only show image if it is sufficiently far away from the others
dist = np.sum((embeddings_2d[i] - shown_images) ** 2, 1)
if np.min(dist) < 2e-3:
continue
shown_images = np.r_[shown_images, [embeddings_2d[i]]]
shown_images_idx.append(i)
# plot image overlays
for idx in shown_images_idx:
thumbnail_size = int(rcp["figure.figsize"][0] * 2.0)
path = os.path.join(path_to_data, filenames[idx])
img = Image.open(path)
img = functional.resize(img, thumbnail_size)
img = np.array(img)
img_box = osb.AnnotationBbox(
osb.OffsetImage(img, cmap=plt.cm.gray_r),
embeddings_2d[idx],
pad=0.2,
)
ax.add_artist(img_box)
# set aspect ratio
ratio = 1.0 / ax.get_data_ratio()
ax.set_aspect(ratio, adjustable="box")
# get a scatter plot with thumbnail overlays
get_scatter_plot_with_thumbnails()
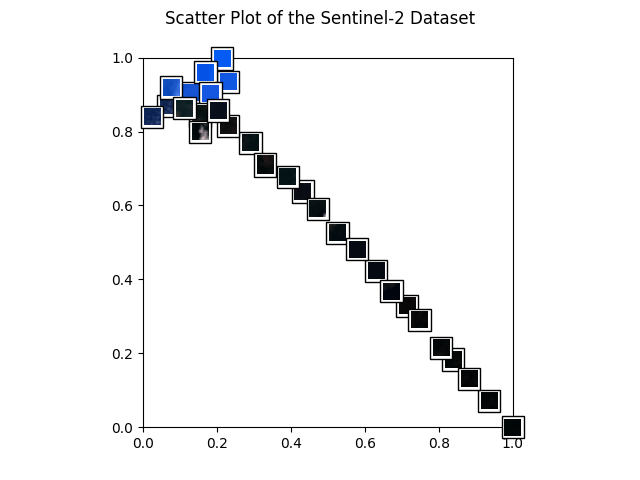
Next, we plot example images and their nearest neighbors (calculated from the embeddings generated above). This is a very simple approach to find more images of a certain type where a few examples are already available. For example, when a subset of the data is already labelled and one class of images is clearly underrepresented, one can easily query more images of this class from the unlabelled dataset.
Let’s get to work! The plots are shown below.
example_images = [
"S2B_MSIL1C_20200526T101559_N0209_R065_T31TGE/tile_00154.png", # water 1
"S2B_MSIL1C_20200526T101559_N0209_R065_T32SLJ/tile_00527.png", # water 2
"S2B_MSIL1C_20200526T101559_N0209_R065_T32TNL/tile_00556.png", # land
"S2B_MSIL1C_20200526T101559_N0209_R065_T31SGD/tile_01731.png", # clouds 1
"S2B_MSIL1C_20200526T101559_N0209_R065_T32SMG/tile_00238.png", # clouds 2
]
def get_image_as_np_array(filename: str):
"""Loads the image with filename and returns it as a numpy array."""
img = Image.open(filename)
return np.asarray(img)
def get_image_as_np_array_with_frame(filename: str, w: int = 5):
"""Returns an image as a numpy array with a black frame of width w."""
img = get_image_as_np_array(filename)
ny, nx, _ = img.shape
# create an empty image with padding for the frame
framed_img = np.zeros((w + ny + w, w + nx + w, 3))
framed_img = framed_img.astype(np.uint8)
# put the original image in the middle of the new one
framed_img[w:-w, w:-w] = img
return framed_img
def plot_nearest_neighbors_3x3(example_image: str, i: int):
"""Plots the example image and its eight nearest neighbors."""
n_subplots = 9
# initialize empty figure
fig = plt.figure()
fig.suptitle(f"Nearest Neighbor Plot {i + 1}")
#
example_idx = filenames.index(example_image)
# get distances to the cluster center
distances = embeddings - embeddings[example_idx]
distances = np.power(distances, 2).sum(-1).squeeze()
# sort indices by distance to the center
nearest_neighbors = np.argsort(distances)[:n_subplots]
# show images
for plot_offset, plot_idx in enumerate(nearest_neighbors):
ax = fig.add_subplot(3, 3, plot_offset + 1)
# get the corresponding filename
fname = os.path.join(path_to_data, filenames[plot_idx])
if plot_offset == 0:
ax.set_title(f"Example Image")
plt.imshow(get_image_as_np_array_with_frame(fname))
else:
plt.imshow(get_image_as_np_array(fname))
# let's disable the axis
plt.axis("off")
# show example images for each cluster
for i, example_image in enumerate(example_images):
plot_nearest_neighbors_3x3(example_image, i)
Next Steps
Interested in exploring other self-supervised models? Check out our other tutorials:
Total running time of the script: (72 minutes 35.987 seconds)




