Selection Algorithm
Application and Order of Strategies
Generally, the order in which the different strategies were defined in the config does not matter.
- In a first step, all the thresholding strategies are applied.
- In the next step, all other strategies are applied in parallel.
Different tasks can also be combined. E.g. you can use predictions from
"my_weather_classification_task"for one strategy combined with predictions from"my_object_detection_task"from another strategy.
The LightlyOne optimizer tries to fulfill all strategies as well as possible.
Potential reasons why your objectives were not satisfied:
- Tradeoff between different objectives. The optimizer always has to tradeoff between different objectives. E.g. it may happen that all samples with high
WEIGHTSare close together. If you also specified the objectiveDIVERSITY, then only a few of these high-weight samples may be chosen. Instead, also other samples that are more diverse, but have lower weights, are chosen. You can control the relative importance of the objectives with thestrengthparameter of each strategy. - Restrictions in the input dataset. This applies especially for
BALANCE: For example, if there are only 10 images of ambulances in the input dataset and a total of 1000 images are selected, the output can only have a maximum of 1% ambulances. Thus aBALANCEtarget of having 20% ambulances cannot be fulfilled. - Too few samples to choose from. If the selection algorithm can only choose a small number of samples, it may not be possible to fulfill the objectives. You can solve this by increasing
n_samplesorproportion_samples.
Strategy Strength
Each selection strategy (except Threshold, see above for the reason) has an optional strength configuration property, which sets its relative strength compared to the other strategies. The default is 1.0. Negative strengths are allowed and will invert the strategy. Only the relative values of the strategies to each other matter, e.g. strengths of 1 and 2 for two strategies each have the same effect as strategy strengths of 10 and 20 each.
See below for example use cases. This config option is available since worker version 2.8.2.
Add a tiny bit of randomness as a "tie-breaker" if multiple samples have the same objective score:
// Select images with the highest number of objects.
{
"input": {
// for worker >=2.11
"type": "PREDICTIONS",
"task": "my_object_detection_task",
"name": "CATEGORY_COUNT",
// for worker <2.11
"type": "SCORES",
"task": "my_object_detection_task",
"score": "object_frequency,
},
"strategy": {
"type": "WEIGHTS"
}
},
// Add a bit of random noise to select randomly if multiple
// images have the same number of objects.
{
"input": {
"type": "RANDOM",
},
"strategy": {
"type": "WEIGHTS",
"strength": 0.01,
}
},
Enforce balancing across video metadata:
// Select the same number of frames from every video by setting a high strength.
{
"input": {
"type": "METADATA",
"key": "video_name",
},
"strategy": {
"type": "BALANCE",
"target": {
video_name: 1/len(videos) for video_name in videos
},
"strength": float(1e9),
}
},
// Within the same video, select the most diverse frames by setting a low strength
// to give this strategy less importance than the balancing strategy.
{
"input": {
"type": "EMBEDDINGS",
},
"strategy": {
"type": "DIVERSITY",
"strength": 1.0,
}
}Prefer dark images by selecting samples with low luminance:
{
"input": {
"type": "METADATA",
"key": "lightly.luminance",
},
"strategy": {
"type": "WEIGHTS",
"strength": -1.0,
}
}For numerical reasons, there are two restrictions for the strength parameter:
- It must be in [-1e9, 1e9].
- The ratio between the highest and lowest strength must be smaller than 1e10. E.g. if you have a strategy with a strength of 1e9, the other strategies should have a strength whose absolute value is at least 0.1.
Selection Algorithm
The LightlyOne selection algorithm selects the samples greedily, i.e. one sample after the other. This is the only algorithm that can scale to millions of samples.
In each step, it selects the samples that lead to the highest fulfillment of the overall selection objective. The overall objective is the product of the objectives of each strategy. Taking the product has the advantage that the scale of each strategy objective is irrelevant, as multiplying all scores of one strategy by a constant has the same effect as multiplying the overall scores by a constant: It does not change the order of the overall scores.
This is shown in the example below with a Visual Diversity and Active Learning strategy. The visual diversity strategy computes how well each sample fulfills the visual diversity objective. At the same time, the active learning strategy computes how well the active learning score objective is fulfilled. Consider a case with 3 samples:
| Visual Diversity Objective | Active Learning Score Objective | Overall Score | |
|---|---|---|---|
| sample 1 | 21.0 | 10.3 | 216.30 |
| sample 2 | 20.8 | 10.8 | 224.64 |
| sample 3 | 20.5 | 10.9 | 223.45 |
The sample selected by the LightlyOne selection algorithm is sample 2 in this case, as it has the highest overall score.
The strategy strength of each strategy is applied as the exponent of the strategy objective: overall_score = product(strategy.objective ^ strategy.strength for strategy in strategies).
Thresholding is done before the combination selection process, thus it is excluded in the combination selection of the other strategies.
Strategy Objectives
In every step of the selection process, each strategy calculates for each unselected sample, which objective value it would cause if it was selected. The definition of the objective depends on the type of strategy.
Diversity
The Diversity strategy has the objective of maximizing the sum of diversities between samples. The diversity of a sample is the distance from it to its closest neighbor in the embedding space. The following plot visualizes the objective as the sum of the lengths of the green lines.
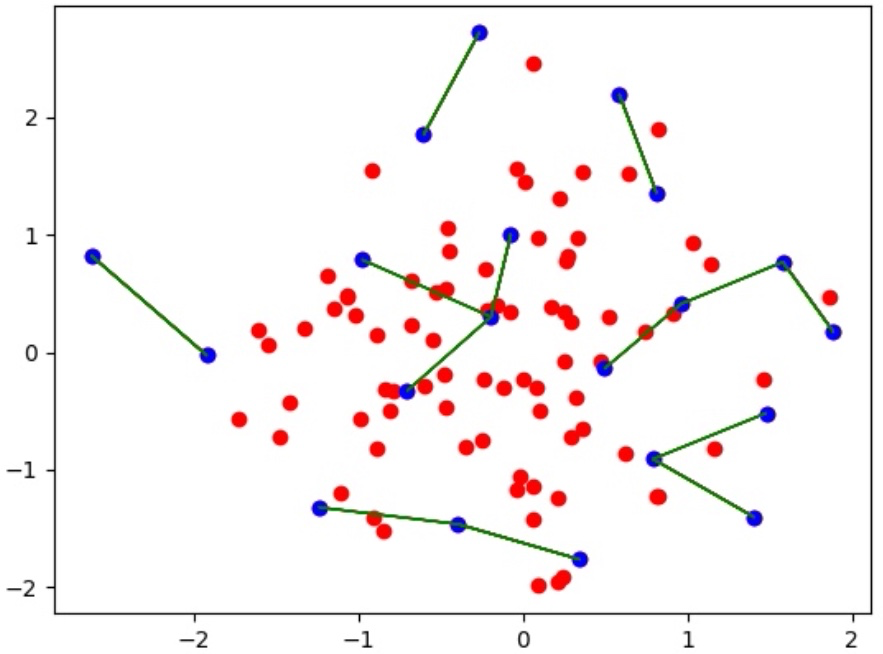
Distance between selected samples (blue) is depicted as green lines. Red samples are unselected samples.
Weights
Weighting has the objective of maximizing the sum of input values of the selected samples. E.g. if the selected samples have inputs values of 1, 2, and 0.5 respectively, then the objective value is 1+2+0.5=3.5.
Typicality
Typicality has the objective of maximizing the sum of typicalities of the selected samples. E.g. if the selected samples have typicality values of 0.7, 0.3, and 0.2 respectively, then the objective value is 0.7+0.3+0.2=1.2.
Balance
The Balance strategy aims to maximize the similarity between the distribution of the selected samples and the target distribution.
We calculate the objective as 1 / CrossEntropy(distribution_selected_samples, target_distribution).
In each selection step, it is calculated for each new sample, which new distribution among selected samples it would cause if it was selected, and which new objective value this would cause. As new samples might worsen the distribution, the objective value can decrease.
Similarity
The Similarity strategy first calculates the maximum cosine similarity from each sample to the key samples. Then it treats this similarity similar to the Weights strategy and has the objective of maximizing the sum of similarities.
Updated 4 months ago
